Enthalpie
Die Energiemenge, die ein System bei konstantem Druck als Wärme an die Umgebung abgibt oder von ihr aufnimmt, wird Reaktionsenthalpie ΔH genannt.
Man kann nur Energieänderungen messen, daher Δ.
Folgender Versuch soll den Begriff Enthalpie, der schon auf der vorigen Seite erklärt wurde, näher erläutern:
Bildung eines gasförmigen Reaktionsproduktes:
Zink + Salzsäure → Zinkchlorid + Wasserstoff / exotherm
Situation 1:

- Hahn geschlossen
- geschlossenes System
- exotherme Reaktion
Das Volumen (V) bleibt konstant. Obwohl sich der Druck im System erhöht, kann das entstehende Gas keine Volumenarbeit verrichten.
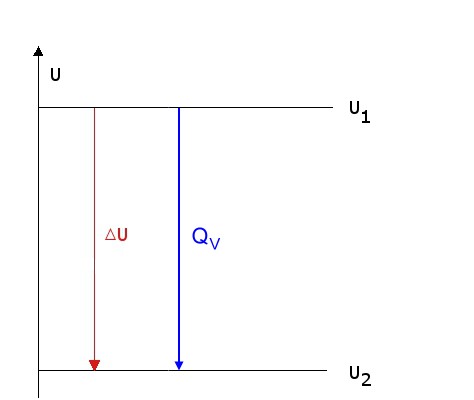
Die Reaktionswärme(QV) der exothermen Reaktion ist gleich der Reaktionsenergie bzw. der Änderung der Inneren Energie.
QV = ΔrU
Energiediagramm
Zusammenhang zwischen Innerer Energie und Reaktionsenergie bei konstantem Volumen:
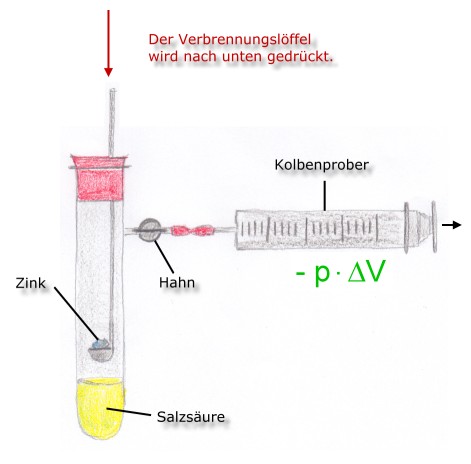
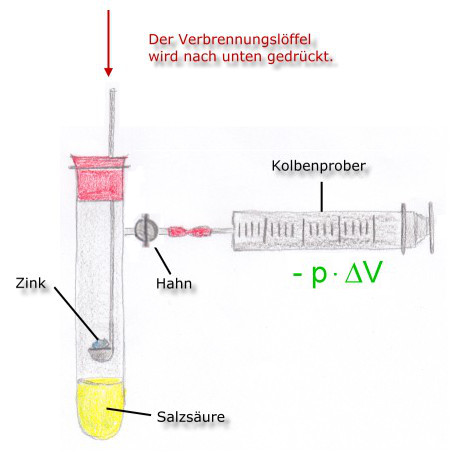
Situation 2:
- Hahn geöffnet
- annähernd adiabatisches System
- exotherme Reaktion
Der Druck bleibt im Reagenzglas konstant, da sich das entstehende Gas (Wasserstoff) ausdehnen kann, wobei es Arbeit verrichtet.
In diesem Fall entspricht die Reaktionswärme nicht der Inneren Energie. Da ein Anteil an Arbeitsenergie dem System verloren geht, gilt:
ΔrU = Qp - p · ΔV
Formt man die Gleichung nach Qp um, so ergibt sich:
Qp = ΔU + p · ΔV
Die Zustandsgrößen U, p und V werden zu einer neuen Zustandsgröße zusammengefasst:
Der Reaktionsenthalpie (ΔrH).
ΔrH = Qp = ΔU + p · ΔV
Die Enthalpieänderung entspricht also unter dieser Bedingung der Reaktionswärme Qp.
Energiediagramm
Zusammenhang zwischen Innerer Energie und Reaktionsenergie
bei konstantem Druck und Volumenarbeit (W = p ⋅ ΔV):
Vergleich der Systeme
U = Innere Energie
Q = Reaktionswärme
H = Enthalpie
Reaktionen, in denen Gase verwendet werden oder entstehen
| Systeme | abgeschlossen | geschlossen | offen | adiabatisch |
| Stoffaustausch | nein | nein | ja | nein |
| Energieaustausch | nein | ja | ja | nein |
| Volumen konstant | ja | ja | nein | nein |
| Druck konstant | nein | nein | ja | ja |
| Zusammenhang | Q = U | Q = U | Q = H | Q = H |
Reaktionen, bei denen keine Gase verwendet werden oder entstehen
| Systeme | abgeschlossen | geschlossen | offen | adiabatisch |
| Stoffaustausch | nein | nein | (nein)1) | |
| Energieaustausch | nein | ja | ja | |
| Volumen konstant | ja | ja | ja | |
| Druck konstant | ja | ja | ja | |
| Zusammenhang | Q = H = U | Q = H = U | Q = H = U |
1)Lässt man ein Weinglas lange offen stehen, so bildet sich Essig. Ob bei einem offenen System, bei dem keine Gase entstehen, tatsächlich kein Stoffaustausch stattfindet, muss im Einzelfall diskutiert werden.
Die Enthalpie eines stofflichen Systems vergrößert sich, wenn die Reaktion endotherm verläuft, das stoffliche System also Energie in Form von Wärme aus der Umgebung aufnimmt:
ΔrH > 0
Gibt das stoffliche System Energie in Form von Wärme an die Umgebung ab, so ist ist die Reaktion exotherm:
ΔrH < 0