Momentangeschwindigkeit
Reaktionsgeschwindigkeit zu einem bestimmten Zeitpunkt
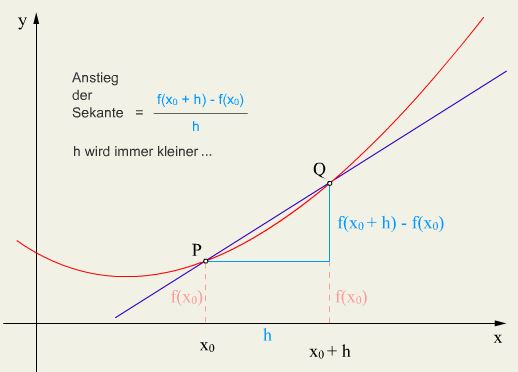
Wie wir gesehen haben, verändert sich die Reaktionsgeschwindigkeit im Verlauf der Zeit. Um die momentane Geschwindigkeit zu einem bestimmten Zeitpunkt zu ermitteln – zum Beispiel die Anfangsgeschwindigkeit, müsste das Zeitintervall beliebig klein gewählt werden, was mathematisch durch folgende Gleichung ausgedrückt wird (Bildung von Differentiale):
(sprich: „Δc nach Δt“), f´(t), c´
Diesen Differentialquotienten nennt man auch 1. Ableitung der Funktion f. Die 1. Ableitung beschreibt die Änderungsrate einer gegebenen Funktion zu einem exakten Zeitpunkt. Der Differentialquotient entspricht der Steigung der Tangente in einem Punkt.
Hilfen zum Differentialquotienten
Animation von www.mathe-online.at, welche die Änderung von Sekanten- und Tangentensteigung verdeutlicht.
In der Animation wird deutlich, dass wenn h (=Δx, bei unserem Konzentrations- / Zeitdiagramm wäre dies Δt) gegen Null geht, die Sekante zur Tangente wird (Ableitung).
Siehe auch den externen Link hier.
Die Steigung der Tangente gibt die Momentangeschwindigkeit an.
c/t-Diagramm
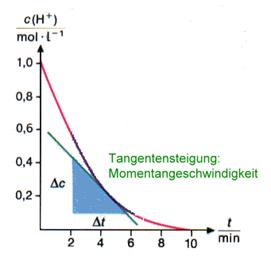
Die Tangente bzw. die Senkrechte zur Tangente kann man mit Hilfe eines Tricks konstruieren. Siehe hierzu den externen Link:
