Während also, wie zuvor erläutert, die Reaktionszeit von der Menge der Ausgangsstoffe abhängig ist, bezieht sich die Reaktionsgeschwindigkeit auf eine Konzentrationsänderungwährend eines bestimmten Zeitraumes.
Prinzipiell kann man die Reaktionsgeschwindigkeit
in einem bestimmten Zeitraum messen (mittlere Reaktionsgeschwindigkeit) oder aber
zu einem x-beliebigen Zeitpunkt (Momentangeschwindigkeit), wobei
die Messung der Anfangsgeschwindigkeit eine besondere Momentangeschwindigkeit darstellt.
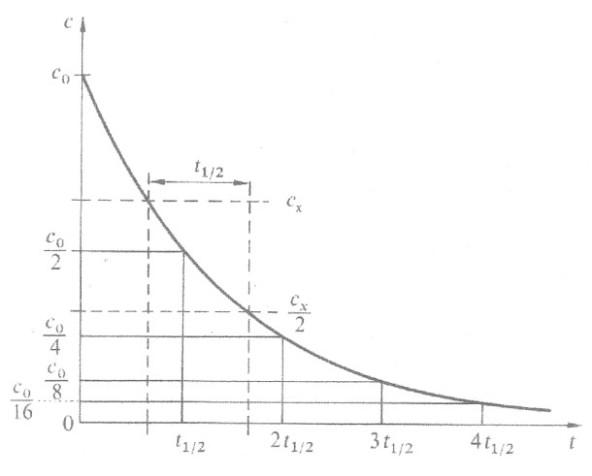
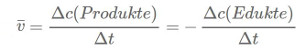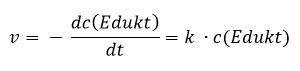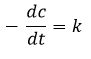Reaktionsgeschwindigkeit für eine bestimmte Zeitspanne
Die mittlere Reaktionsgeschwindigkeit ist der Quotient aus der Konzentrationsänderung Δc und der dafür benötigten Zeitspanne Δt. Entsprechend kann man die Reaktionsgeschwindigkeit auch als die Abnahme der Konzentration eines Ausgangsstoffes beziehen. Da Reaktionsgeschwindigkeiten keinen negativen Wert haben können, setzt man vor dem Quotienten vereinbarungsgemäß ein Minuszeichen.
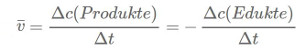
Dabei ist es gleichgültig, welche der an der Reaktion beteiligten Stoffe man betrachtet, da alle Stoffe über die stöchiometrische Gleichung miteinander verbunden sind.
Folgende Reaktion, bei der die Konzentrationsabnahme von Wasserstoff-Ionen (pH-Wert-Messung, Messung der elektrischen Leitfähigkeit) bzw. die Wasserstoffentwicklung gemessen werden kann, soll das verdeutlichen:
Nehmen wir noch einmal das Beispiel "Reaktion von Zink mit Salzsäure" vom Beitrag Reaktionszeit.
Bei dieser Reaktion nimmt auf der Eduktseite die Konzentration an Wasserstoff-Ionen ab, auf der Produktseite nimmt die Konzentration an Zink-Ionen zu. Die entscheidenden Teilchen, die wir für den Verlauf der Reaktion betrachten sind also:
2 H+ + Zn → H2+ Zn2+ (Zn im Überschuss = konst.)
Für die Bildung von einem Mol Zink(II)-Ionen werden zwei Mol Wasserstoff-Ionen verbraucht. Die Konzentration an Wasserstoff-Ionen nimmt also doppelt so schnell ab, wie die Konzentration an Zink(II)-Ionen zunimmt:
⭐ Warum steht hier H3O+ in der Gleichung?
Während nach Arrhenius die "Säureteilchen" die Wasserstoff-Ionen, also Protonen darstellen, sind es nach Brönsted die Oxonium-Ionen (H3O+), also protonierte Wassermoleküle.
Die Abhängigkeit einer Größe von einer anderen Größe kann man durch eine Funktion f(x) ausdrücken. Jeder Eingangsgröße (Argument, meist x) ist eine Ausgangsgröße (Funktionswert, meist y) zugeordnet. Eine Funktion kann graphisch dargestellt werden.
Konzentrations/Zeit-Diagramme (c/t-Diagramm)
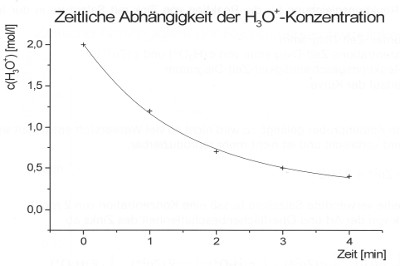
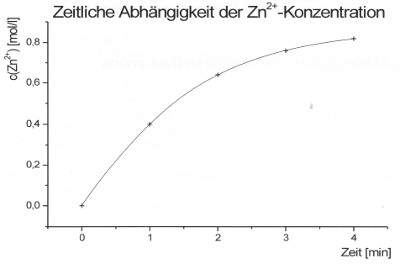
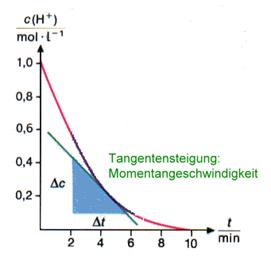
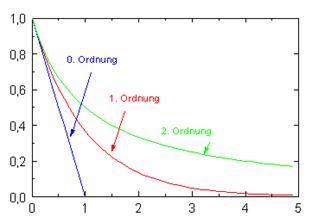
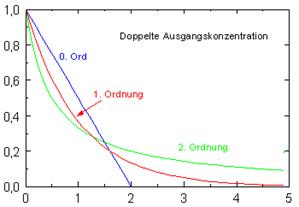
Hier ist die Konzentrationsabnahme von Wasserstoff-Ionen (Protonen) bzw. Oxonium-Ionen dargestellt. Der Funktionsgraph zeigt eine exponentielle Abklingfunktion. Für die Zunahme der Zink(II)-Ionenkonzentration ergibt sich eine spiegelbildliche Sättigungskurve.
Eine chemische Reaktion, wie die Reaktion einer Säure mit einem unedlen Metall verläuft also zu Beginn am schnellsten.
⭐ Wie ermittelt man die Konzentrationen der Oxonium-Ionen und Zink-Ionen zu einem bestimmten Zeitpunkt?
Zur Messung der Reaktionsgeschwindigkeit wird man denjenigen Reaktionspartner heranziehen, dessen Konzentrationsänderung sich am leichtesten ermitteln lässt. Ändert sich zum Beispiel die Konzentration an Wasserstoff-Ionen oder anderen Ionen, kann die pH-Wert-Messung bzw. die laufende Bestimmung der elektrischen Leitfähigkeit als Methode herangezogen werden. Ist ein Reaktionspartner farbig, gestattet die Bestimmung der Lichtabsorption der Lösung dessen Konzentrationsbestimmung in Abhängigkeit von der Zeit.
Auch die Entnahme von Proben nach verschiedenen Zeiten mit anschließender Titration wäre möglich.
Da die Stoffmenge eines Gases in einem Volumen bekannt ist (Molvolumen idealer Gase), kann man aus dem Volumen des entstehenden Wasserstoffs die Oxonium-Ionen-Konzentration berechnen.
Beispiel:
Stoffmengenkonzentration der Salzsäure zu Beginn des Versuchs sei 2 mol/l. Es werden 5 ml Salzsäure und überschüssiges Zink verwendet. Die Messung erfolgt unter SATP-Bedingungen (298,15 K = 25° C; 1013 hPa ≈ 1 bar). Unter diesen Bedingungen beträgt das Molvolumen eines idealen Gases rund 24,5 Liter.
Zum Zeitpunkt t= 3 Minuten wurde ein Volumen von 85 ml gemessen.
Berechnen Sie die Stoffmengenkonzentration von Oxonium-Ionen zu diesem Zeitpunkt.
Lösung: [Der Lösungsweg ist für registrierte Nutzer ab Benutzergruppe 1 (einfach registrierte Lehrer ohne Schulbescheinigung) und für meine Lerngruppen in Q4 sichtbar]
Die Stoffmengenkonzentration an Oxonium- bzw. Wasserstoff-Ionen beträgt nach 3 Minuten 0,6124 mol/l.
Die Stoffmengenkonzentration an Zink-Ionen beträgt nach 3 Minuten 0,6938 mol/l.
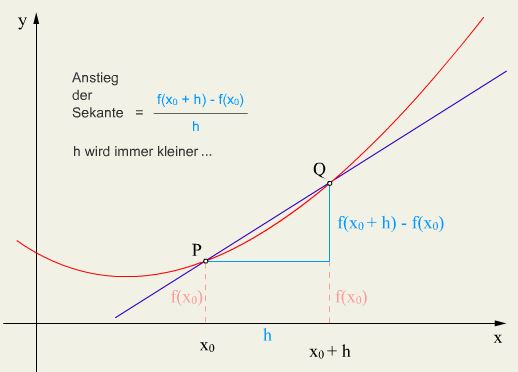
Der Differenzenquotient ist graphisch betrachtet die Steigung der Sekante. Die Steigung der Sekante gibt die mittlere Reaktionszeit an.
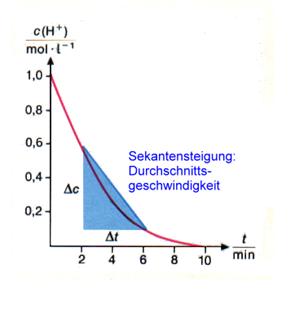
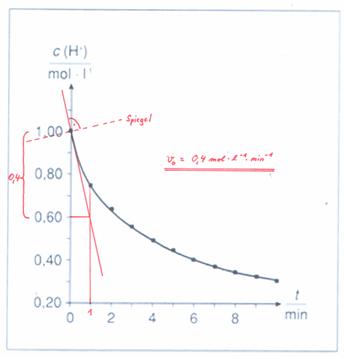
Die Steigung der Sekante, also die Reaktionsgeschwindigkeit in diesem Zeitabschnitt, ist zu Beginn der Reaktion am größten. Ist ja auch klar: Gibt man Zink in Salzsäure, so ist die Gasentwicklung zu Beginn am größten - dann nimmt sie zunehmend ab.
Die Reaktionsgeschwindigkeit ist in der Regel von den Konzentrationen der Reaktionsteilnehmer abhängig. Da sich die Konzentrationen während der hier betrachteten Reaktion mit zunehmender Reaktionszeit immer langsamer verändern, ändert sich auch die Reaktionsgeschwindigkeit entsprechend. Da die Konzentration der Ausgangsstoffe abnimmt, nimmt hier auch die Reaktionsgeschwindigkeit ab.
Reaktionsgeschwindigkeit zu einem bestimmten Zeitpunkt
Wie wir gesehen haben, verändert sich die Reaktionsgeschwindigkeit im Verlauf der Zeit. Um die momentane Geschwindigkeit zu einem bestimmten Zeitpunkt zu ermitteln – zum Beispiel die Anfangsgeschwindigkeit, müsste das Zeitintervall beliebig klein gewählt werden, was mathematisch durch folgende Gleichung ausgedrückt wird (Bildung von Differentiale):
(sprich: „Δc nach Δt“), f´(t), c´
Diesen Differentialquotienten nennt man auch 1. Ableitung der Funktion f. Die 1. Ableitung beschreibt die Änderungsrate einer gegebenen Funktion zu einem exakten Zeitpunkt. Der Differentialquotient entspricht der Steigung der Tangente in einem Punkt.
In der Animation wird deutlich, dass wenn h (=Δx, bei unserem Konzentrations- / Zeitdiagramm wäre dies Δt) gegen Null geht, die Sekante zur Tangente wird (Ableitung).
Interessant ist die Ermittlung der Anfangsgeschwindigkeit einer Reaktion aus vielen Gründen. Zwei Beispiele:
Die Reaktion wird durch die entstehenden Produkte bzw. durch das „Verschwinden“ der Edukte noch nicht so stark beeinträchtigt.
Es gibt drei grundsätzliche Muster (Reaktionsordnungen, Zeitgesetze), nach denen eine Reaktion verlaufen kann. Man unterscheidet zwischen 0. Ordnung, 1. Ordnung und 2. Ordnung. c/t-Diagramm (Hier sind die Konzentrationsänderungen bei unterschiedlichen Zeitgesetzen gegen die Reaktionszeit aufgetragen worden.)
Ein Vergleich dieser Graphen zeigt: Zu Beginn nimmt die Reaktionsgeschwindigkeit bei allen Reaktionsordnungen annähernd linear ab. Die Anfangsgeschwindigkeit ist demnach unabhängig von dem weiteren Reaktionsverlauf und damit unabhängig von einer Reaktionsordnung.
Wird eine Messung bei einer langsamen Reaktion am Anfang der Reaktion gemacht, kann man davon ausgehen, dass der Differenzenquotient die Anfangsgeschwindigkeit für diese Reaktion ist.
Die Reaktionsgeschwindigkeit ist proportional zur Konzentration der Ausgangsstoffe.
Betrachten wir einen einfachen Fall: Ein Edukt reagiert zu einem Produkt. In diesem Fall ist die Reaktionsgeschwindigkeit ausschließlich von der Konzentration c des Eduktes abhängig. Der proportionale Zusammenhang zwischen der Reaktionsgeschwindigkeit und der Konzentration des Eduktes nennt man Geschwindigkeitsgleichung oder auch Zeitgesetz:
k ist der Proportionalitätsfaktor (Geschwindigkeitskonstante).
Sind mehrere Edukte bei der Reaktion beteiligt, so gilt:
Die Summe der Exponenten stellt die sogenannte Reaktionsordnung dar.
Die Geschwindigkeitskonstante k ist ein Maß für den Abbau bzw. Bildung der entsprechenden Stoffe. Je größer die Geschwindigkeitskonstante ist, desto schneller verläuft die Reaktion.
Die Reaktionsordnung lässt sich nur experimentell ermitteln. Sie ist aus einem Reaktionsschema nicht abzuleiten.
c/t-Diagramme
0. Ordnung
Die Stoffmengenabnahme ist linear fallend.
Die Reaktionsgeschwindigkeit ist unabhängig von der Konzentration konstant und nur von der Geschwindigkeitskonstante abhängig:
Eine doppelte Menge verdoppelt auch die Reaktionszeit.
Beispiele:
Geschwindigkeit der Aufnahme oder Ausscheidung eines Medikamentes, Ethanolabbau in der Leber, Ansteigen der Blutspiegelkurve bei intravenöser Tropfinfusion, Elektrolysen. Oft auch katalytische Prozesse wie z.B. die Zersetzung von Stickstoffmonooxid zu Stickstoff und Sauerstoff mittels Gold als Katalysator:
2 N2O(g)→ 2 N2(g) + O2(g)
1. Ordnung
Die Stoffmengenabnahme ist anfangs groß, dann allmählich abnehmend (exponentielle Abklingkurve).
Die Reaktionsgeschwindigkeit ist direkt proportional zur Konzentration eines Stoffes:
Die Reaktionszeit ist unabhängig von der Ausgangskonzentration
Die doppelte Menge hat keinen Einfluss auf die Reaktionszeit!
Beispiel:
Zerfallsreaktion von Stickstoffpentoxid 2 N2O5(g)→ 4 NO2(g) + O2
2. Ordnung
Die Stoffmengenabnahme ist anfangs groß, dann allmählich abnehmend - aber nicht exponentiell, sondern sie dauert mit Fortschreiten der Reaktionszeit immer länger.
Die Reaktion ist entweder zum Quadrat der Konzentration eines Stoffes proportional oder prpportional zum Produkt der Konzentrationen zweier Stoffe.
Die doppelte Menge führt zu einem dramatischen Anstieg der Anfangsreaktionsgeschwindigkeit. Es wird schneller eine niedrigere Konzentration erreicht.
Zur Untersuchung eines Stoffes wird die Reaktion oft mit einem Überschuss des anderen Stoffes durchgeführt, um das einfache Geschwindigkeitsgesetz 1. Ordnung zu erhalten. Man spricht dann von einer pseudo 1. Ordnung.
Die Zeit, nach der die Hälfte des Eduktes abgebaut ist, nennt man Halbwertszeit t1/2.
Ein typisches Merkmal einer Reaktion, die nach dem Zeitgesetz 1. Ordnung verläuft, ist die Tatsache, dass die Halbwertszeiten t1/2, t1/4, t1/8, t1/16 usw. gleich sind. Das kann man in einem c/t-Diagramm einfach ablesen:
Die Halbwertszeit einer Reaktion 1. Ordnung ist demnach unabhängig von der Konzentration des Ausgangsstoffes.
