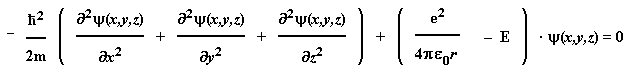Der Weg zur Orbitaltheorie
In einem Doppelspaltversuch kann man zeigen, dass sowohl Licht, als auch Elektronen ein Interferenzmuster auf dem Schirm ergeben. Das gleiche Phänomen beobachtet man bei Schall- oder Wasserwellen.


 Wie können Elektronen Eigenschaften von Wellen haben, wo wir sie uns doch - wie Niels Bohr es tat - als Teilchen vorstellen?
Wie können Elektronen Eigenschaften von Wellen haben, wo wir sie uns doch - wie Niels Bohr es tat - als Teilchen vorstellen?
Ein ähnliches Problem ergibt es auch beim Licht. Schon im 17. Jahrhundert hatte NEWTON seine Gesetze der Optik unter der Voraussetzung gemacht, dass Licht aus Teilchen besteht.
EINSTEIN stellte sich 1905 Licht aus Lichtquanten, so genannten Photonen, vor. Ein Photon stellt eine Energieportion dar (Quantisierung). Demnach kann Licht Energie nur in ganzzahligen Vielfachen dieser Menge aufnehmen oder abgeben. Diese Energie hängt von der Frequenz des Lichtes ab:
(h = Plancksches Wirkungsquantum)
Auf der anderen Seite war gegen Ende des 19. Jahrhunderts mit der Formulierung der Maxwellgleichung klar, dass Licht elektromagnetische Wellen sind, die sich mit Lichtgeschwindigkeit ausbreiten.
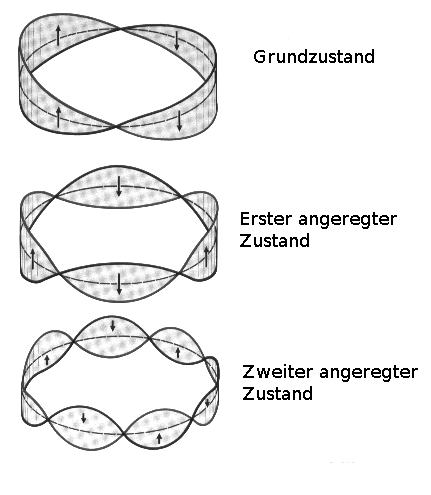
LOUIS VICTOR DE BROGLIE sprach 1922 im Zusammenhang mit Elektronen von so genannten Materiewellen. Damit wären die von BOHR postulierten erlaubten Bahnen ganzzahlige Vielfache der Wellenlänge eines Elektrons (stehende Elektronenwellen).
Eine schwingende Ringsaite:
Was ist nun aber ein Elektron wirklich - Welle oder Teilchen? Ist es ein Teilchen, dass auch Wellencharakter besitzt?
Es hat auf alle Fälle Teilchencharakter, da man die Masse eines Elektrons durch die Ablenkung in einem Magnetfeld messen kann. Sie beträgt ca. 5,5 · 10-4 u. Allerdings ist diese Masse im Verhältnis zur Masse eines Protons oder Neutrons extrem klein, so dass man sie bei einfachen Betrachtungen und Überlegungen vernachlässigt.
1 unit = 1,6605387313 · 10-24 g
Außerdem besitzt ein Elektron eine Ladung. Und es bewegt sich mit einer Geschwindigkeit von 8 Millionen km/h. Doch hier gibt es gleich das nächste Problem. Wie sollte man die Bahnkurve eines Elektrons beobachten, das eine so hohe Geschwindigkeit und eine so geringe Masse besitzt? Dazu müsste man Ort und Geschwindigkeit gleichzeitig messen können.
 HEISENBERG erkannte 1927 in seiner Unschärferelation, dass es im Mikrokosmos unmöglich ist, Ort und Geschwindigkeit gleichzeitig zu bestimmen.
HEISENBERG erkannte 1927 in seiner Unschärferelation, dass es im Mikrokosmos unmöglich ist, Ort und Geschwindigkeit gleichzeitig zu bestimmen.
Vergleichen lässt sich das mit einer Fotographie eines Rennautos. Bei kleiner Belichtungszeit kann ich nur den Ort des Wagens bestimmen. Bei großer Belichtungszeit kann ich nicht den genauen Ort angeben. Dafür kann ich dann die Geschwindigkeit durch das "Verschwimmen" des Bildes erkennen.
Für Elektronen lassen sich also Aufenthaltsort und Geschwindigkeit (bzw. Impuls) auch bei genauesten Messungen prinzipiell nur mit einer gewissen Unschärfe angeben. Wäre die Beobachtung eines Elektrons durch ein (Elektronen)Mikroskop möglich, so führte bereits die Einstrahlung von Licht zu einer Änderung der Geschwindigkeit des Elektrons. Die Messapparatur beeinflusst das Objekt selbst.

Die wichtigste Konsequenz dieser Unschärferelation ist: Atommodelle müssen ohne die Vorstellung von Elektronenbahnen auskommen. Es lassen sich jedoch Aufenthaltsräume angeben, in denen Elektronen mit bestimmter Wahrscheinlichkeit anzutreffen sind. Sie heißen Orbitale. Die Berechnungen dieser Aufenthaltsräume gelang 1926 dem Physiker SCHRÖDINGER mit Hilfe von komplizierten Wellenfunktionen. Dieses wellenmechanische Modell integriert die beiden Vorstellungen von Teilchen und Welle. Man bezeichnet es als Orbital-Modell.
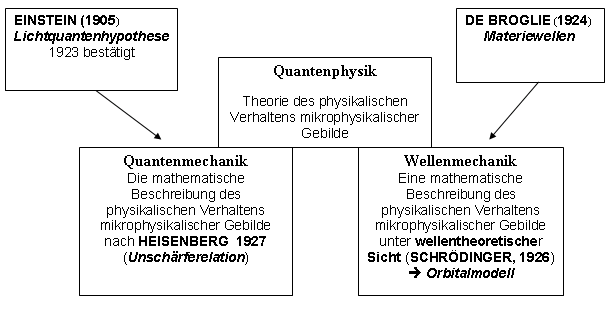
Überblick der Entwicklung:
Schrödinger-Gleichung für das Wasserstoff-Atom:
bzw.